ルクセンの独り言。

音楽とアイドルとテニスとラーメンと数学が好きなオタクの独り言。

『むてきのうた』は「無敵の歌」(3)

前回(『むてきのうた』は「無敵の歌」(2) - ルクセンの独り言。)は2種類の4度について複素数平面で考察しました。
これについて少し追加があるので今回はそれを紹介したいと思います。
新しい発見や後に繋がる考察はないです。
ただ単にネイピア数を登場させたかっただけのブログなので読み飛ばして頂いても構いません。

 

◆オイラーの公式

まずオイラーの公式の話を大雑把にしていきます。

{e}^xをマクローリン展開すると
{{e}^x}=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\cdots
(いやぁ…この時点で綺麗ですよねえ、ネイピア数…)
x=i\theta (\theta\in\mathbb{R})を代入して
{e}^{i\theta}=1+\frac{i\theta}{1!}+\frac{{(i\theta)}^2}{2!}+\frac{{(i\theta)}^3}{3!}+\frac{{(i\theta)}^4}{4!}+\frac{{(i\theta)}^5}{5!}+\cdots
=1+\frac{i\theta}{1!}-\frac{{\theta}^2}{2!}-\frac{i{\theta}^3}{3!}+\frac{{\theta}^4}{4!}+\frac{i{\theta}^5}{5!}-\cdots
=(1-\frac{{\theta}^2}{2!}+\frac{{\theta}^4}{4!}-\cdots)+i(\frac{\theta}{1!}-\frac{{\theta}^3}{3!}+\frac{{\theta}^5}{5!}-\cdots)
ここで、\sin{x},\cos{x}をそれぞれマクローリン展開すると
\sin{x}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots
\cos{x}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots
であるから
{e}^{i\theta}=\cos{\theta}+i\sin{\theta}
が成り立ちます。これがオイラーの公式です。
今回は使いませんが、特に\theta=\piのとき
{e}^{i\pi}+1=0
が成り立ちます(オイラーの等式)。
博士の愛した数式です。
ネイピア数、虚数単位、円周率を繋ぐ何とも美しい等式です。

 

◆例のコード進行をネイピア数で

ということで、オイラーの公式を使えば複素数をネイピア数を用いて表せそうです。
あらかじめ断っておくと、この作業は恐らく今後全く意味をなさないと思います。
ですが、ただ単にネイピア数が好きなのでやってみたいと思います。

前回のブログの数列\{z_n\}において、z_nを極形式で表すと
{z_1}=\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi,
{z_n}={(\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi)}^n\cdot(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})[n=2,3,\cdots,7]
ド・モアブルの定理から
{z_n}={(\cos\frac{5n}{6}\pi+i\sin\frac{5n}{6}\pi)}\cdot(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})[n=2,3,\cdots,7]
したがって、オイラーの公式から\{z_n\}はネイピア数eを用いて
{z_1}={e}^{i\frac{5}{6}\pi},
{z_n}={e}^{i\frac{5n+1}{6}\pi}[n=2,3,\cdots,7]
と表されます。
ネイピア数、虚数単位、円周率、アイドルを繋ぐ非常に美しい式になりましたね。
ちなみに、恐らくアイドルにネイピア数を関連付けたのは世界で僕が初なので、僕は来年あたりフィールズ賞を貰うと思います。

 


はい、という訳で今回はこんなところで。
次回は「完璧じゃないからこその美しさ」についてお話ししたいと思います。
それではまた、ごきげんよう。

『むてきのうた』は「無敵の歌」(2)

前回(『むてきのうた』は「無敵の歌」(1) - ルクセンの独り言。)はコード進行について数列を用いて考察しました。

そこでキーとなりそうなことが分かった「4度」について深く考察していきたいと思います。

 

◆完全4度と増4度

同じ「4度」にも、「完全4度」 の他に「増4度」というものがあります。

 

詳しい話はググって頂きたいのですが、

大雑把に言うと

 

完全4度上→半音×5上の音

増4度上→半音×6上の音

 

です。

 

◆複素数平面と4度

同じ4度にも「完全4度」「増4度」があると言いました(本当は「減4度」もありますが)。

それを可視化していきたいと思います。

 

以下、角度を弧度法で表記します。

f:id:rukusen-rukusen:20170923161505j:image 

複素数平面上に原点Oを中心とする半径1の円をかき、点E♭を(1,0)にとります。

そこから半音上がるたびに\frac{\pi}{6}回転するように点E♭, F, G, A♭, B♭, C, Dをとります。

 

このとき、iを虚数単位として、

E♭=1

F=\frac{1}{2}+\frac{\sqrt{3}}{2}i

G=-\frac{1}{2}+\frac{\sqrt{3}}{2}i

A♭=-\frac{\sqrt{3}}{2}+\frac{1}{2}i

B♭=-\frac{\sqrt{3}}{2}-\frac{1}{2}i

C=-i

D=\frac{\sqrt{3}}{2}-\frac{1}{2}i

の複素数を得ます。また、便宜上これらを順に{p_1},{p_2},\cdots,{p_7}とします。

 

すると、代理コードで置き換えたコード進行を

複素数の数列

p_4,p_7,p_3,p_6,p_2,p_5,p_1

で表せます。

これを数列\{z_n\}(n=1,2,\cdots,7)とすると

{z_1}=-\frac{\sqrt{3}}{2}+\frac{1}{2}i

複素数平面上においてz_2はz_1を\pi回転させたもの、すなわち\frac{5}{6}\pi回転させた後さらに\frac{\pi}{6}回転させたものであるから

{z_2}={z_1}\cdot(\cos\frac{5}{6}\pi+i\sin\frac{5}{6}\pi)\cdot(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})

={z_1}\cdot{z_1}\cdot(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})

={z_1}^2\cdot(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6})

(※後々わかりやすいように\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}は極形式のまま残してます。)

以降\frac{5}{6}\piずつ回転させるから、以下が得られます。

{z_1}=-\frac{\sqrt{3}}{2}+\frac{1}{2}i

{z_n}={z_1}^n\cdot(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}) (n=2,3,\cdots,7)

 

こうしてみた時に、やっぱり気になるのが\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}の部分です。

これ、何なんでしょうか？

これが無かったら{z_n}=(-\frac{\sqrt{3}}{2}+\frac{1}{2}i)^nとなって、なおかつ-\frac{\sqrt{3}}{2}+\frac{1}{2}iは完全4度だからめちゃくちゃ綺麗だったのに。

 

もうお気づきですか？

 

完全4度をさらに\frac{\pi}{6}回転する、すなわち完全4度+半音上です。

 

そうです。

 

ここで増4度の登場です。

 

では、増4度はいったいどんな響きなのでしょう。

周波数比は32/45と非常に複雑です。

完全4度で規則正しく回転する中に、1小節だけこの複雑なコードのイレギュラーが入ります。

 

規則正しいのに一つだけ必ずしも綺麗ではないコードが入ることによって、2小節目でどこか「不安感」や「物寂しさ」を感じます。また、しばしばオンコードにすることでそれが強調されます。

 

この「不安感」を感じるイレギュラーこそが、この進行が「エモい」最たる所以なのです。

 

かなり長くなってしまったので、続きはまた次回お話しましょう。

『むてきのうた』は「無敵の歌」(1)

せっかくブログを開設したので

記事を書いてみます。

 

ときめき♡宣伝部の3rdシングル

『むてきのうた』 をご存知でしょうか。

 

 

むてきのうた(どきどき盤)(DVD付)

むてきのうた(どきどき盤)(DVD付)

 

 

 

僕はこの曲が大好きです。

 

もはや ときめき♡宣伝部 よりも好きです。

(嘘です。)

 

かなみんのパート割が極端に少ないこと以外は

100点満点中800点くらいだと思ってます。

とにかく作詞・作曲・MVなど

どこを取っても良いんですよ。

(語彙力の無さを恨む)

 

その良さについて僕なりに考察してみたので

これから数回に分けて書いていこうかなと。

 

まず今回は音楽理論的な

「コード進行が美しい」という話から。

 

◆王道進行

『むてきのうた』においてキーとなるコード進行があります。

それは

A♭→B♭/A♭→Gm→Cm→Fm→B♭→E♭

という7小節からなる進行です(特に前半4小節は王道進行と呼ばれます)。

これは『むてきのうた』に限らずJPOPで多用されるコード進行です。

 

このコード進行、とても興味深いので今回は数学で考察してみます。

 

「音楽なのに数学？」と思うかもしれません。

ですがこの進行、数学的にアプローチするととてもおもしろいんです。

 

◆音楽的アプローチ

とは言いつつ、ひとまず音楽的にみていきます。

 

前半4小節はBメロやサビでよく用いられます。

年代を問わず、日本のポップソングで多用されます。

適当に数曲選べば1曲はこれを使っているのではないか、というくらい頻出です。

 

なぜこれほど多用されるか。

それは盛り上がるということ、

それに所謂「エモい」曲調になりやすいことに起因すると僕は考えます。

 

そして5・6小節目は「ツーファイブ」「強進行」と呼ばれ、4度上に移動することで自然にコードをつなぎ、盛り上げる効果があるらしいです。

 

この2つの組み合わせなので、『むてきのうた』のキーのコード進行は非常に盛り上がるコード進行ともいえます。

 

◆コード進行と数列

あとで数学的知識の補足ブログを掲載するので、ここではその辺を割愛させていただきます。

 

という訳で、数学的にアプローチしていきます。

コード進行を数学的に処理するために、コード進行を数列に変換したいと思います。

また、単純化するためにコードの根音を考えることとします。

f:id:rukusen-rukusen:20170918151738j:image

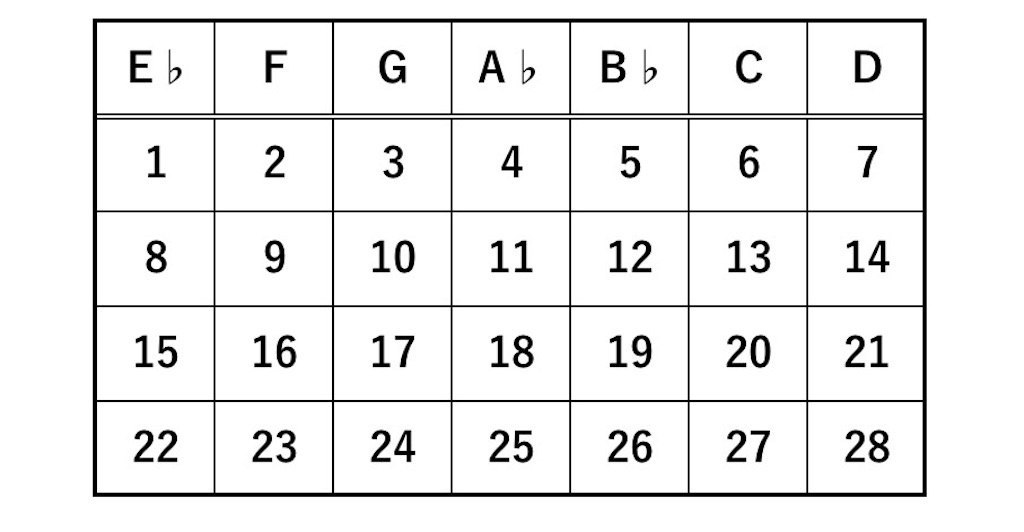
【変換規則】

①表の縦の数字がそれぞれコードに対応

②1小節前の数字より大きい数字を用いる

③上の2つを満たす数字のうち最小の数字を用いる

 

この規則に従い変換すると以下の数列\{a_n\}を得ます。

4,5,10,13,16,19,22

 

話は一旦逸れますが、コードには「代理コード」というものがあります。

これは、その名の通り「代理可能なコード」です。

 

具体的には

ⅠとⅢm、Ⅵm

ⅣとⅡm

ⅤとⅦm7♭5

などです。

 

この代理コードの考えを使うと

B♭≒Dm7♭5

とできます。

 

B♭を代理コードで置き換えた数列\{a'_n\}は以下のようになります。

4,7,10,13,16,19,22

これは初項4、公差3の等差数列ですね♪

必要ありませんが、ついでに一般項も出してみますか。

a'_n=4+(n-1)・3=3n+1

公差3ということは4度ずつ上がってるってことです。

これがめちゃくちゃ美しいんです。

 

なんでかって？

 

それでは次の章でお話しいたしましょう。

 

◆2音の周波数比

「度」とは何か、という説明も割愛させていただきます。気になる方はググってください。

 

ある音 と、そのn度上の和音との周波数比は以下となります。 

 

f:id:rukusen-rukusen:20170921200113j:image

 

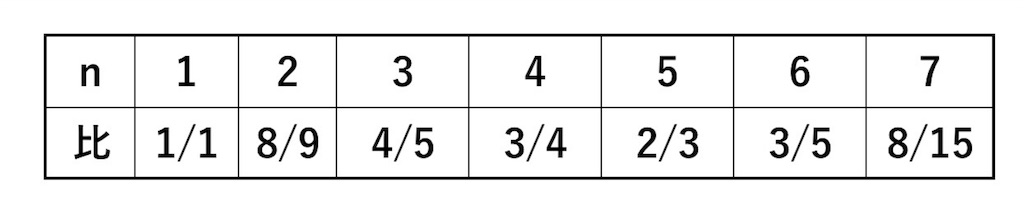
このうち簡単な整数比である4度と5度の音を「完全4度」「完全5度」と言います。

 

一般的に比が簡単になるほど綺麗な響きになります。

 

以上のことから、このコード進行はとてもスムーズに綺麗な響きを持って規則正しく移動しているコード進行と考えられます。

 

 

長くなったので続きはまた次回。

次回は「4度」についてもう少し掘り下げて、また数学的にもアプローチしてみます。